Perceptron, MLP and XOR problem
Motivation
Ok, one step before Neuron Networks, what is basically the core for any modern Reinforcement Learning algorithms is perceptron. Why do we need Neuron Networks? so Linear functions are good, but it is not enough to approximate and generalise data with non-linear and complex patterns. Neuron Network consists of Neurons obviously, but then what is neuron?
Neuron it is a Perceptron + Non linear activation function.
AND,OR,XOR logic operations
Before we proceed, let just remember what is logical operations AND, OR and XOR. We will need it later and you will see why. If you pass any informatica exams or you are familiar with programming languages you should be familiar with it. 0 is equivalent of False, 1 is equivalent of True. 2 examples for OR: (0 or 0)=0 (False or False = False) and (0 or 1)=1 (False or True = True), ... and other is by analogy. Revise for AND and XOR by yourself!
or | and | xor
x1 x2 y | x1 x2 y | x1 x2 y
0 0 0 | 0 0 0 | 0 0 0
0 1 1 | 0 1 0 | 0 1 1
1 0 1 | 1 0 0 | 1 0 1
1 1 1 | 1 1 1 | 1 1 0
Let's back to the Perceptron.
Perceptron
What is perceptron then? Perceptron it is linear predictor with weights and bias (via linear regression our previous post) + activation function on top of it.
Properties:
- Binary output 0 or 1;
- No Non-linear activation function (step function).
Perceptron value given x1 and x2 as features is equation of a line V = w1 * x1+w2 * x2+b, where w and b are weights and bias of perceptron and x1,x2 are features of the object and after we pass this V value through activation function we and get an output 0 or 1 as output what can be interpreted as one of classes type.
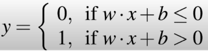
Perceptron as simple supervised machine learning model that can be used as binary classifier.
For instance, we have a task to predict color of the point. For example, we have two types of points blue and white one (picture below). Each point has its own features, aka characteristics which describes their position on Decart (Cartesian) coordinates. Where each point uniquely defined as a pair of real numbers called (x,y) or (x1,x2) coordinates. Picture below:
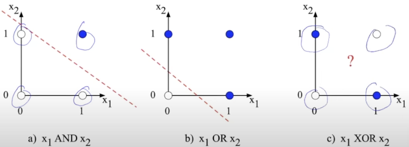
Here is an interesting moment. We can use single perceptron to classify points on pictures a) anb b) and spoiler not in c). So why is it? How to predict correct point types for AND and OR?.
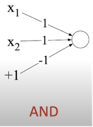
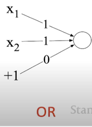
Values which you can see on picture 1 and 0 are weights and biases of this single unit perceptron. We can't say now how to find them and let's think that they are given. The thing we have to concentrate now is that we get correct predictions!
Ok, but which x1, and x2 to use? The answer is simple - coordinates of the points from the Picture 1. But if you look at points carefully you can notice one interesting thing. They are equivalent to logical operations!! Each graphic a),b),c) have 4 points and each of logical operation has 4 cases! They are the same (Picture 1.). So Picture 1 is graphical visualisation of logical operations OR, And and XOR
or | and | xor
x1 x2 y | x1 x2 y | x1 x2 y
0 0 0 | 0 0 0 | 0 0 0
0 1 1 | 0 1 0 | 0 1 1
1 0 1 | 1 0 0 | 1 0 1
1 1 1 | 1 1 1 | 1 1 0

Single perceptron allows us to build one line for binary classification task. Everything what is below line belongs to one class everything what is above are points of another class. On the c) picture you can notice that points can't be correctly split into two classes by one line, you need more lines or compress the plane. But how we can do it? using MLP!!!
Multi-Layer Perceptron (MLP)
Demonstration of the need in Multi-Layer Perceptron (MLP) - many layers of Perceptrons in a row came by Minsky and Papert in 1969 that single perceptron can’t calculate a simple XOR function, but MLP can and it is already almost Feed Forward Neuron Network. We ommit here moment how to train it (will be in the next chapter of this course), but MLP already is able correctly classify points on picture c. To understand how it is done is the main goal of this lesson.
So classification of points for XOR using MLP is called XOR problem - It is a nice visualisation why do we actually need MLP and Neuron Networks - to build Machine Learning models that can solve complex tasks which can't be solved by other ML models.
Now we know why we need this, let's now understand how it works and implement this calculation on python!
One more thing which will be useful is knowlege about Relu activation function. Relu f(x)=max(0,x), other words if x<=0 Relu value is 0 else x.
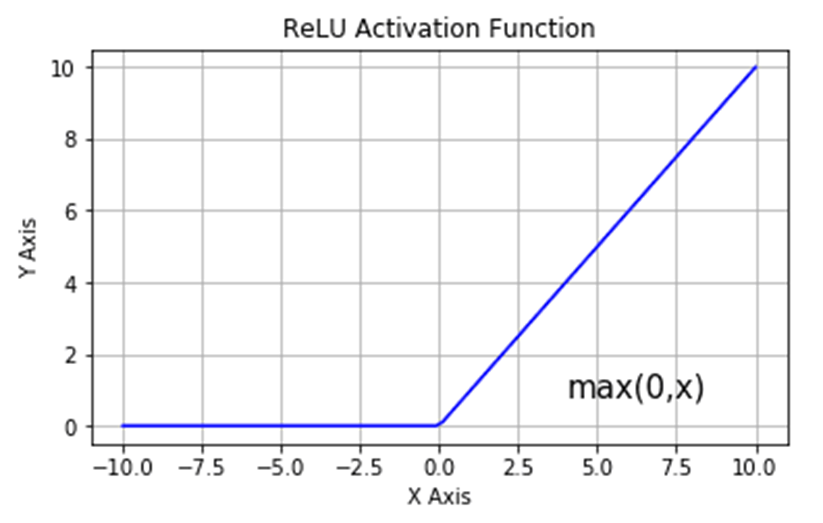
Inside relu as x value we will pass perceptron output value.
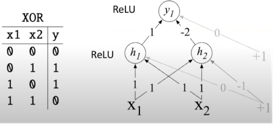
Example of how XOR can be calculated with a few perceptrons (3 perceptrons on the Picture 3.) and ReLU non-linear activation function XOR can’t be calculated by a single perceptron XOR can be calculated by a layered network of units.
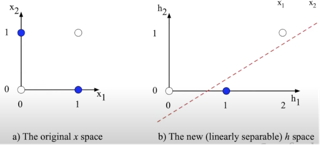
The hidden representation of after the first layer is on the Picture 4. We spent on it 2 out of 3 layers of our MLP. And we can see that this graphical points we already can correctly split into 2 classes with one line using our last 3td perceptron. Cool again, right?
So if you pass this values through all 3 perceptron you will get correct answers for XOR problem. What is good.
We set up correct weights manually in this example. In Neuron Network they will be learning during training process. With XOR theory we are done! The last step is to code perceptron and MLP for solving xor problem.
Perceptron python code
import numpy as np
class Perceptron:
def __init__(self, weights: np.array, bias: int):
self.weights = weights
self.bias = bias
def __call__(self, input_: np.array, b: int = 0):
return np.dot(input_, self.weights) + self.bias * b
@staticmethod
def relu(input_: int):
return np.array(max(0, input_))
@staticmethod
def step(input_: int):
return 0 if input_ <= 0 else 1
class LogicOperationMLP:
def __init__(self, x):
self.x = x
@staticmethod
def or_(x:list):
p = Perceptron(weights=np.array([1, 1]), bias=0)
output = p.step(p(input_=x, b=1))
print(f"{x[0]} {x[1]} {output}")
@staticmethod
def and_(x:list):
p = Perceptron(weights=np.array([1, 1]), bias=-1)
output = p.step(p(input_=x, b=1))
print(f"{x[0]} {x[1]} {output}")
@staticmethod
def xor(x:list):
def mlp(x_, h1, h2, y1):
h1_ = h1.relu(h1(x_, b=1))
h2_ = h2.relu(h2(x_, b=1))
x_ = np.array([h1_, h2_])
output = y1.relu(y1(x_, b=1))
return output
# init weights in perceptron, according to the pictures above
h1 = Perceptron(weights=np.array([1, 1]), bias=0)
h2 = Perceptron(weights=np.array([1, 1]), bias=-1)
y1 = Perceptron(weights=np.array([1, -2]), bias=0)
print(f"{x[0]} {x[1]} {mlp(x, h1, h2, y1)}")
if __name__ == '__main__':
lo = LogicOperationMLP(x=np.array([[0, 0],
[0, 1],
[1, 0],
[1, 1]]))
print("or\nx1 x2 y")
for input_ in lo.x:
lo.or_(x=input_)
print("and\nx1 x2 y")
for input_ in lo.x:
lo.and_(x=input_)
print("xor\nx1 x2 y")
for input_ in lo.x:
lo.xor(x=input_)
# output
# or | and | xor
# x1 x2 y | x1 x2 y | x1 x2 y
# 0 0 0 | 0 0 0 | 0 0 0
# 0 1 1 | 0 1 0 | 0 1 1
# 1 0 1 | 1 0 0 | 1 0 1
# 1 1 1 | 1 1 1 | 1 1 0
We are done! Now we know what is perceptron and Neuron (perceptron+non-linear activation function) and Neuron Network (MLP). And now we are ready to start learning how to train Neuron Network and get those parameters that were given to us here by default.